[06 Feb 2020] Check for balanced parentheses in an expression

Check for balanced parentheses in an expression

Given an expression string exp , write a program to examine whether the pairs and the orders of “{“,”}”,”(“,”)”,”[“,”]” are correct in exp.

Example:

Input: exp = “[()]{}{[()()]()}”
Output: Balanced

Input: exp = “[(])”
Output: Not Balanced

Algorithm:

• Declare a character stack S.
• Now traverse the expression string exp.
  1. If the current character is a starting bracket (‘(‘ or ‘{‘ or ‘[‘) then push it to stack.
  2. If the current character is a closing bracket (‘)’ or ‘}’ or ‘]’) then pop from stack and if the popped character is the matching starting bracket then fine else parenthesis are not balanced.
• After complete traversal, if there is some starting bracket left in stack then “not balanced”

Below image is a dry run of the above approach:

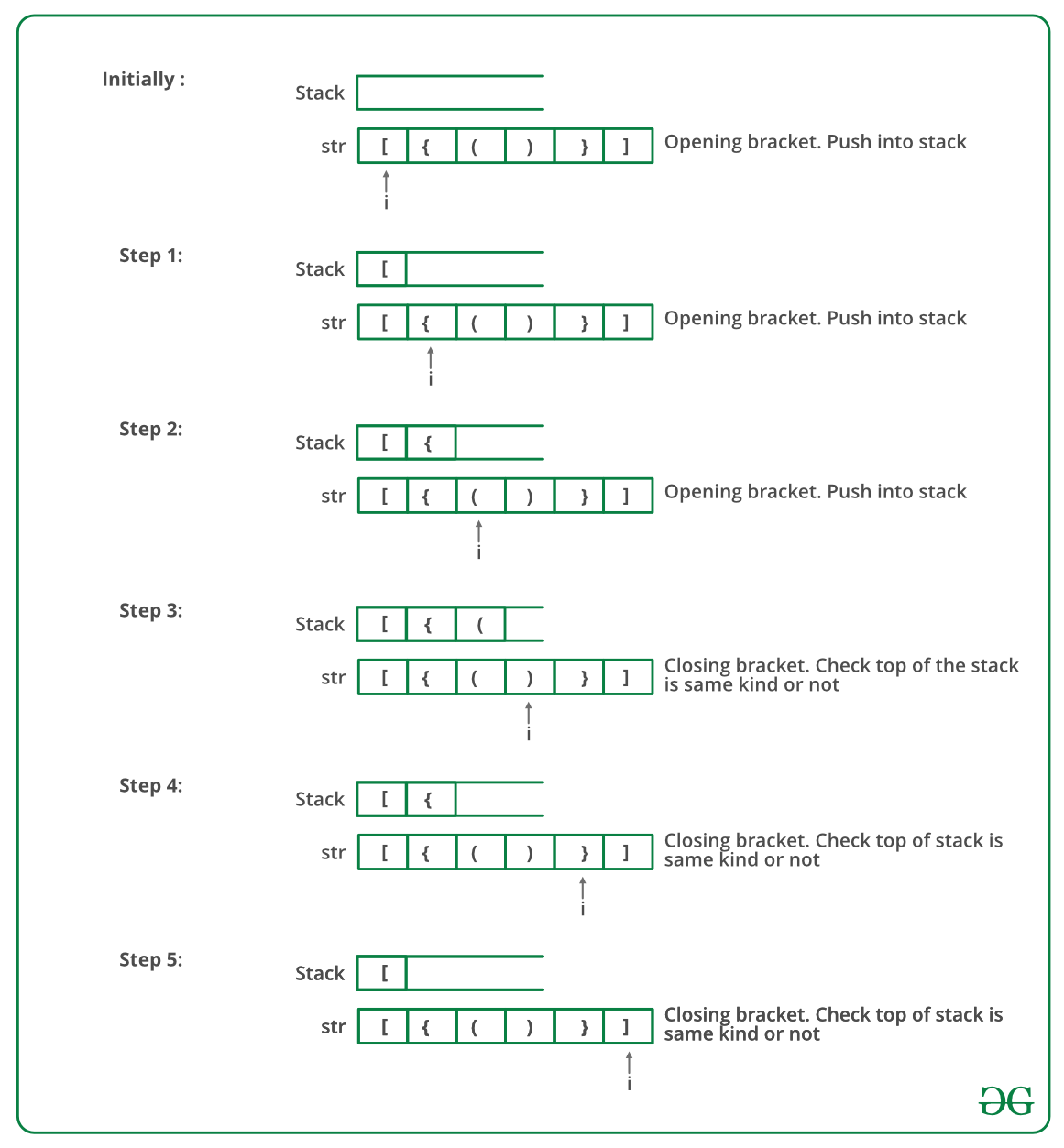
Below is the implementation of the above approach:

// CPP program to check for balanced parenthesis. #include<bits/stdc++.h> using namespace std;    // function to check if paranthesis are balanced bool areParanthesisBalanced(string expr) {     stack<char> s;     char x;        // Traversing the Expression     for (int i=0; i<expr.length(); i++)     {         if (expr[i]=='('||expr[i]=='['||expr[i]=='{')         {             // Push the element in the stack             s.push(expr[i]);             continue;         }            // IF current current character is not opening         // bracket, then it must be closing. So stack         // cannot be empty at this point.         if (s.empty())            return false;            switch (expr[i])         {         case ')':                // Store the top element in a             x = s.top();             s.pop();             if (x=='{' || x=='[')                 return false;             break;            case '}':                // Store the top element in b             x = s.top();             s.pop();             if (x=='(' || x=='[')                 return false;             break;            case ']':                // Store the top element in c             x = s.top();             s.pop();             if (x =='(' || x == '{')                 return false;             break;         }     }        // Check Empty Stack     return (s.empty()); }    // Driver program to test above function int main() {     string expr = "{()}[]";        if (areParanthesisBalanced(expr))         cout << "Balanced";     else         cout << "Not Balanced";     return 0; }

Output:

Balanced

Time Complexity: O(n)
Auxiliary Space: O(n) for stack.

# Python3 program to check for # balanced parenthesis.     # function to check if  # paranthesis are balanced  def areParanthesisBalanced(expr) :         s = [];         # Traversing the Expression      for i in range(len(expr)) :            if (expr[i] == '(' or              expr[i] == '[' or expr[i] == '{') :                # Push the element in the stack              s.append(expr[i]);              continue;             # IF current character is not opening          # bracket, then it must be closing.           # So stack cannot be empty at this point.          if (len(s) == 0) :             return False;             if expr[i] == ')' :                # Store the top element in a              x = s.pop();                            if (x == '{' or x == '[') :                 return False;             elif expr[i] == '}':                 # Store the top element in b              x = s.pop();                            if (x == '(' or x == '[') :                 return False;                     elif x == ']':                 # Store the top element in c              x = s.pop();                            if (x =='(' or x == '{') :                 return False;         # Check Empty Stack      if len(s) :         return True     else :         return False    # Driver Code if __name__ == "__main__" :         expr = "{()}[]";         if (areParanthesisBalanced(expr)) :         print("Balanced");      else :         print("Not Balanced");     # This code is contributed by AnkitRai01

Output:

Balanced

Time Complexity: O(n)
Auxiliary Space: O(n) for stack.

// Java program for checking // balanced Parenthesis    public class BalancedParan  {     static class stack      {         int top=-1;         char items[] = new char[100];            void push(char x)          {             if (top == 99)              {                 System.out.println("Stack full");             }              else              {                 items[++top] = x;             }         }            char pop()          {             if (top == -1)              {                 System.out.println("Underflow error");                 return '\0';             }              else              {                 char element = items[top];                 top--;                 return element;             }         }            boolean isEmpty()          {             return (top == -1) ? true : false;         }     }            /* Returns true if character1 and character2        are matching left and right Parenthesis */     static boolean isMatchingPair(char character1, char character2)     {        if (character1 == '(' && character2 == ')')          return true;        else if (character1 == '{' && character2 == '}')          return true;        else if (character1 == '[' && character2 == ']')          return true;        else          return false;     }            /* Return true if expression has balanced         Parenthesis */     static boolean areParenthesisBalanced(char exp[])     {        /* Declare an empty character stack */        stack st=new stack();                /* Traverse the given expression to            check matching parenthesis */        for(int i=0;i<exp.length;i++)        {                        /*If the exp[i] is a starting              parenthesis then push it*/           if (exp[i] == '{' || exp[i] == '(' || exp[i] == '[')             st.push(exp[i]);                   /* If exp[i] is an ending parenthesis               then pop from stack and check if the               popped parenthesis is a matching pair*/           if (exp[i] == '}' || exp[i] == ')' || exp[i] == ']')           {                                   /* If we see an ending parenthesis without                   a pair then return false*/              if (st.isEmpty())                {                    return false;                }                       /* Pop the top element from stack, if                  it is not a pair parenthesis of character                  then there is a mismatch. This happens for                  expressions like {(}) */              else if ( !isMatchingPair(st.pop(), exp[i]) )                {                    return false;                }           }                     }                   /* If there is something left in expression            then there is a starting parenthesis without            a closing parenthesis */                 if (st.isEmpty())          return true; /*balanced*/        else          {   /*not balanced*/              return false;          }      }             /* UTILITY FUNCTIONS */     /*driver program to test above functions*/     public static void main(String[] args)      {         char exp[] = {'{','(',')','}','[',']'};           if (areParenthesisBalanced(exp))             System.out.println("Balanced ");           else             System.out.println("Not Balanced ");       }    }

Output:

Balanced

Time Complexity: O(n)
Auxiliary Space: O(n) for stack.