[04 Feb 2020] Longest Common Subsequence

Longest Common Subsequence
Examples:
LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.
LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.

1) Optimal Substructure:
Let the input sequences be X[0..m-1] and Y[0..n-1] of lengths m and n respectively. And let L(X[0..m-1], Y[0..n-1]) be the length of LCS of the two sequences X and Y. Following is the recursive definition of L(X[0..m-1], Y[0..n-1]).

If last characters of both sequences match (or X[m-1] == Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])

If last characters of both sequences do not match (or X[m-1] != Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2]) )

Examples:
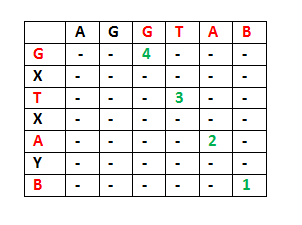
1) Consider the input strings “AGGTAB” and “GXTXAYB”. Last characters match for the strings. So length of LCS can be written as:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)

2) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFHR”), L(“ABCDGH”, “AEDFH”) )

So the LCS problem has optimal substructure property as the main problem can be solved using solutions to subproblems.

2) Overlapping Subproblems:
Following is simple recursive implementation of the LCS problem. The implementation simply follows the recursive structure mentioned above.

/* A Naive recursive implementation of LCS problem */

#include <bits/stdc++.h> 

using namespace std;   

int max(int a, int b);  

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */

int lcs( char *X, char *Y, int m, int n )  

{  

    if (m == 0 || n == 0)  

        return 0;  

    if (X[m-1] == Y[n-1])  

        return 1 + lcs(X, Y, m-1, n-1);  

    else

        return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));  

}  

/* Utility function to get max of 2 integers */

int max(int a, int b)  

{  

    return (a > b)? a : b;  

}  

/* Driver code */

int main()  

{  

    char X[] = "AGGTAB";  

    char Y[] = "GXTXAYB";       

    int m = strlen(X);  

    int n = strlen(Y);       

    cout<<"Length of LCS is "<< lcs( X, Y, m, n ) ;      

    return 0;  

} 

Output:

Length of LCS is 4

# A Naive recursive Python implementation of LCS problem  

def lcs(X, Y, m, n):   

    if m == 0 or n == 0: 

       return 0; 

    elif X[m-1] == Y[n-1]: 

       return 1 + lcs(X, Y, m-1, n-1); 

    else: 

       return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); 

# Driver program to test the above function 

X = "AGGTAB"

Y = "GXTXAYB"

print "Length of LCS is ", lcs(X , Y, len(X), len(Y)) 

Output:

Length of LCS is 4

/* Dynamic Programming C++ implementation of LCS problem */

#include<bits/stdc++.h>  

using namespace std;  

int max(int a, int b);  

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */

int lcs( char *X, char *Y, int m, int n )  

{  

    int L[m + 1][n + 1];  

    int i, j;      

    /* Following steps build L[m+1][n+1] in  

       bottom up fashion. Note that L[i][j]  

       contains length of LCS of X[0..i-1] 

       and Y[0..j-1] */

    for (i = 0; i <= m; i++)  

    {  

        for (j = 0; j <= n; j++)  

        {  

        if (i == 0 || j == 0)  

            L[i][j] = 0;        

        else if (X[i - 1] == Y[j - 1])  

            L[i][j] = L[i - 1][j - 1] + 1;      

        else

            L[i][j] = max(L[i - 1][j], L[i][j - 1]);  

        }  

    }          

    /* L[m][n] contains length of LCS  

    for X[0..n-1] and Y[0..m-1] */

    return L[m][n];  

}  

/* Utility function to get max of 2 integers */

int max(int a, int b)  

{  

    return (a > b)? a : b;  

}  

  

// Driver Code 

int main()  

{  

    char X[] = "AGGTAB";  

    char Y[] = "GXTXAYB";      

    int m = strlen(X);  

    int n = strlen(Y);      

    cout << "Length of LCS is " 

         << lcs( X, Y, m, n );      

    return 0;  

}  

  Output:

Length of LCS is 4

# Dynamic Programming implementation of LCS problem 

  

def lcs(X , Y): 

    # find the length of the strings 

    m = len(X) 

    n = len(Y) 

  

    # declaring the array for storing the dp values 

    L = [[None]*(n+1) for i in xrange(m+1)] 

  

    """Following steps build L[m+1][n+1] in bottom up fashion 

    Note: L[i][j] contains length of LCS of X[0..i-1] 

    and Y[0..j-1]"""

    for i in range(m+1): 

        for j in range(n+1): 

            if i == 0 or j == 0 : 

                L[i][j] = 0

            elif X[i-1] == Y[j-1]: 

                L[i][j] = L[i-1][j-1]+1

            else: 

                L[i][j] = max(L[i-1][j] , L[i][j-1]) 

  

    # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] 

    return L[m][n] 

#end of function lcs   

# Driver program to test the above function 

X = "AGGTAB"

Y = "GXTXAYB"

print "Length of LCS is ", lcs(X, Y)

Output:

Length of LCS is 4